আমরা যেসব ওয়েবসাইট, অ্যাপ, কিংবা সফটওয়্যার ব্যবহার করি তার সবকিছুই তৈরীর পিছনে ছিল কোন না কোন এলগোরিদম। তবে এত হাজারো সাইট বা অ্যাপের মধ্যে আমরা কিন্তু সেটিই ব্যবহার করি যেটি সবচেয়ে দ্রুত রেজাল্ট দেয়। কিন্তু কিভাবে কোন কোড সবচেয়ে দ্রুত একটি রেজাল্ট দিতে পারে তা আমাদের অনেকেরই অজানা।
সেই অজানার সাথেই পরিচয় করানোর প্রত্যাশায় Big O notation এর প্রাথমিক ধারণা তুলে ধরা হয়েছে এ আর্টিকেলে। যেহেতু Big O notation কোন কোডের কস্ট (টাইম, স্পেস) নির্ণয়ের সবচেয়ে সরল উপায়, এর সাথে পরিচিত হওয়ার মাধ্যমে কোডের কার্যকারিতা বাড়ানো বিগিনার কোডারদের জন্য অনেক সহজ হয়ে উঠবে।
Big O notation কী?
এলগোরিদমের কার্যকারিতা নিয়ে ঘাঁটাঘাঁটি করতে গেলে বেশির ভাগ সময় Big O notation এর নাম শোনা যায়। কোন এলগোরিদম কতটা বেশী কার্যকর, তা নির্ণয় করার জন্য সবচেয়ে বেশী জনপ্রিয় টুল হল এই Big O notation। এক কথায় এটি গাণিতিক উপায়ে যে কোন এলগোরিদমের কমপ্লেক্সিটিকে উপস্থাপন করে।
কোডিং এর সাথে আমরা যারা কম বেশী পরিচিত, তারা এটা জানি যে অনেক বড় ইনপুট নানান ভাবে কোডের রানের স্পিডের উপর প্রভাব ফেলে। শুধু তাই নয়, মেমোরিতে সে ঠিক কতটুকু জায়গা দখল করবে তার উপরও প্রভাব ফেলে। কিন্তু ইনপুট বড় নাকি ছোট হবে তা আমরা কখনোই নির্ধারণ করে দিতে পারি না। কারণ যেকোন সিস্টেম তৈরী হয় ইউজারের জন্য। ইউজারের কি ধরণের ইনপুটের রেজাল্ট লাগবে সেটা আগে থেকে জানা মুশকিল।
অতএব, এটি সবসময়ই সত্য যে ইনপুট বড় হতেই পারে। তাহলে কিভাবে সবচেয়ে বড় ইনপুটের জন্যও সবচেয়ে কার্যকর কোড লেখা যায়? যেহেতু আমরা কখনোই ইনপুট বড় হওয়ার হার নিয়ন্ত্রণ করতে পারব না তাহলে অন্য কি উপায়ে কমপ্লেক্সিটি কমানো যেতে পারে?
এসকল প্রশ্নের উত্তর হলো, ইনপুটের বড় হওয়ার হার নিয়ন্ত্রণ করতে না পারলেও এর সাথে কমপ্লেক্সিটি বৃদ্ধির হার নিয়ে কাজের অনেক সুযোগ রয়েছে। ঠিক সে কারণেই ইনপুটের সাথে কমপ্লেক্সিটির গাণিতিক সম্পর্কটা জানা বেশ জরুরী।
ধরে নেই আমরা এমন একটি কাজ করছি যেখানে n সংখ্যক ইনপুট নিলে কমপ্লেক্সিটিও n গুণ বেড়ে যায়। অর্থাৎ n এর সাথে কমপ্লেক্সিটির গুণের সম্পর্ক। আবার কোন কোডের ক্ষেত্রে n সংখ্যক ইনপুটের জন্য কমপ্লেক্সিটি 2n সংখ্যক বেড়ে যায়। অর্থাৎ n এর সাথে কমপ্লেক্সিটির ঘাতের সম্পর্ক। গুণের তুলনায় ঘাতের সম্পর্কে কমপ্লেক্সিটি অনেক তাড়াতাড়ি বেড়ে যায়। যদি n এর মান 5 হয় তাহলে প্রথম শর্তে কমপ্লেক্সিটি বাড়ে ৫ গুণ। আর দ্বিতীয় ক্ষেত্রে ৩২ গুণ !
ঠিক এ সম্পর্কটির একটি সরল এবং সহজবোধ্য রূপ হল এই Big O notation। তাই এটি জানা থাকলেই সহজেই নিজের কোডের কার্যকারিতা নিজেই নির্ণয় করা যায়।
Big O notation কেন গুরুত্বপূর্ণ?
যখন কোন প্রোগ্রামার কোন এলগোরিদম তৈরী করতে চায়, তাকে সর্বপ্রথমেই ভাবতে হয় এর ইনপুট কেমন হতে পারে। তারপর এমন একটি এলগোরিদম ডিজাইন করতে হয়, যা এরকম সকল সম্ভাব্য ইনপুটের জন্য ঠিকমত আউটপুট দিতে পারে। কিন্তু সব রকমের সিস্টেম একই রকমের সুযোগ সুবিধা দিতে পারে না আর সবসময় আউটপুটের জন্য এতটা অপেক্ষা করাও সম্ভবপর হয়ে ওঠে না।
যদি একটি প্রোগ্রামের জন্য ৫১২ মেগাবাইটস বরাদ্দ থাকে, কিন্তু কিছু ইনপুটের ক্ষেত্রে ১ গিগাবাইটস এর আউটপুট দরকার হয়, তবে স্বভাবতই প্রোগ্রামটি ক্র্যাশ করবে। অন্যদিকে যদি একটি কোডের জন্য বরাদ্দকৃত সময় ২ সেকেন্ড থাকে, কিন্তু তা রান করতে ৪ সেকেন্ড সময় নেয়, সে ক্ষেত্রেও ঝামেলা হবে। তাই এলগোরিদমটি একটি নির্দিষ্ট সিস্টেমের জন্য সব ইনপুটে ঠিক রেজাল্ট দিচ্ছে নাকি সেটি যাচাই করা অনিবার্য। এটি ছাড়া কোন সফল এলগোরিদম তৈরী সম্ভব নয়।
শুধু তাই নয়, মানুষের দৈনন্দিন চাহিদা পূরণ করতে একই কাজ সম্পাদনের জন্য তৈরী হচ্ছে অসংখ্য ওয়েবসাইট এবং অ্যাপ। তাই এই প্রতিযোগিতায় টিকতে হলে সে ওয়েবসাইট বা অ্যাপকে হতে হবে অনেক বেশী দ্রুত এবং কার্যকর। সে কারণে প্রায় সকল কোম্পানি প্রতিনিয়ত তাদের সফটওয়্যারের স্পিড বাড়ানোর চেষ্টা করছে। এবং এ স্পিড বাড়ানো কেবল তখনই সম্ভব যখন আমরা এই স্পিড পরিমাপ করতে পারবো, এবং সময় বেশী লাগার কারণ উদ্ধার করতে পারবো।
এ সব কিছুরই সমাধান কেবল Big O notation এর মাধ্যমেই করা সম্ভব। কারণ Big O notation এর মাধ্যমে একটি এলগোরিদম চালাতে কতটুকু সময় বা মেমরি লাগবে তার একটি গাণিতিক ধারণা পাওয়া যায়। তাছাড়া, কোন এলগোরিদম কেন সময় বা মেমোরি বেশী নিচ্ছে সেটিও নির্ণয় করা যায় Big O notation এর ব্যবহারের মাধ্যমে। যেহেতু দ্রুততম এলগোরিদম বানাতে দ্রুততার হিসাবটা আগে জানা প্রয়োজন, তাই কার্যকর এলগোরিদম তৈরীর ক্ষেত্রে Big O notation এর ধারণা থাকা অত্যন্ত প্রয়োজনীয়।
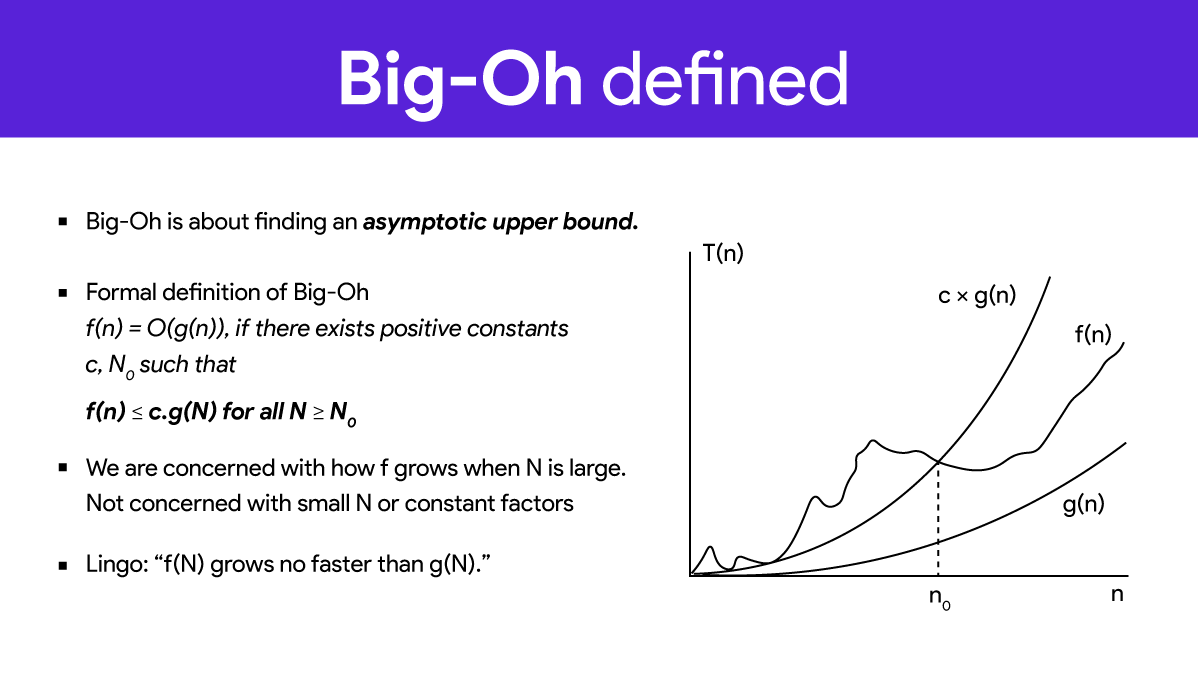
Big O notation এর প্রচলিত সমীকরণ
বিভিন্ন Big O এর কমপ্লেক্সিটি তুলনা
Big O সাধারণত আপার বাউন্ড নিয়ে কাজ করে। এবং এটি কমপ্লেক্সিটির একটি উপস্থাপনা হলেও এটি পুরোপুরি সঠিক কমপ্লেক্সিটি নয়। বরং একটি ধারণা দেয় কেবল। যেমন কোন কোডের কমপ্লেক্সিটি প্রকৃতপক্ষে n2 + 2n + 5. সেক্ষেত্রে Big O এর উপস্থাপনা হবে O(n2)। এতে করে কমপ্লেক্সিটিনিয়ে কাজ করা অনেক সহজ হয়ে যায়। কারণ এক্ষেত্রে কমপ্লেক্সিটির সরাসরি তুলনা করা অনেক সহজ।
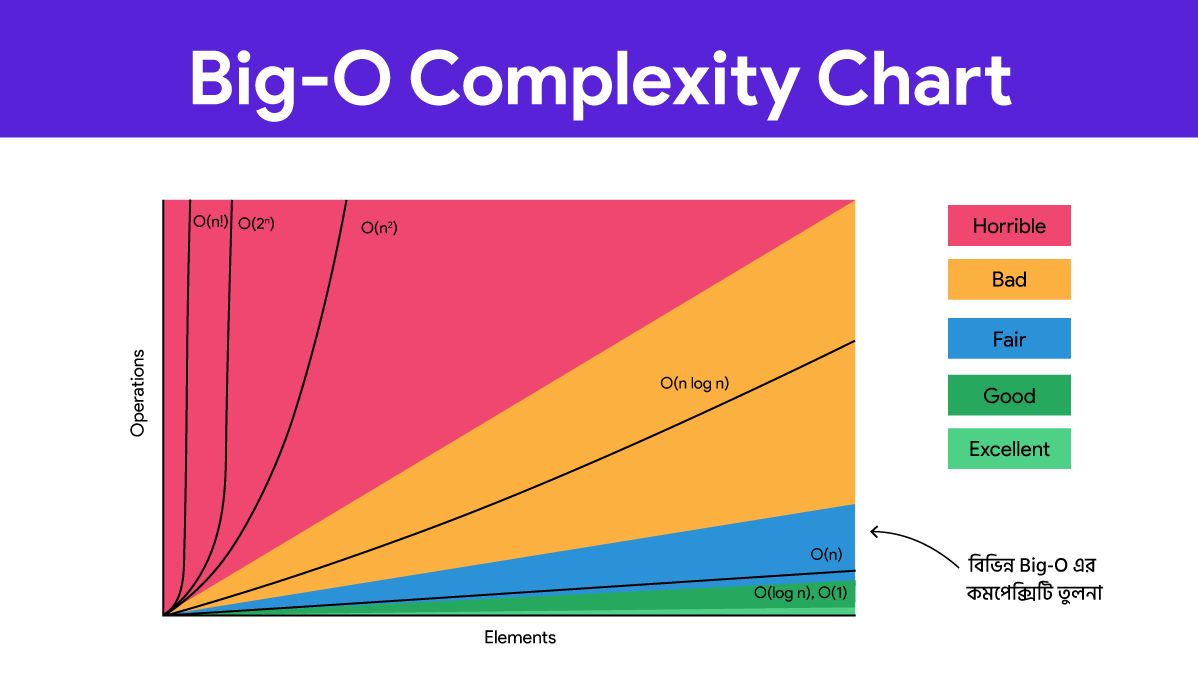
এমনকি অধিক কম্পলেক্স কোডের সরল সমাধান নিয়ে ভাবাও অনেক সহজ হয়। তাই এখানে অধিক ব্যবহৃত বিভিন্ন Big O উপস্থাপনার কমপ্লেক্সিটি নিয়ে আলোচনা করা হল।
O(1) এর কমপ্লেক্সিটি
এ ধরণের কোডের কমপ্লেক্সিটি কন্সট্যান্ট কমপ্লেক্সিটি বলে। এটিকে কিছুক্ষেত্রে সর্বনিম্ন কমপ্লেক্সিটিও বলা যায়। এটির মানে হল এই যে ইনপুট সাইজ যতই বড় হোক, বা যা কিছুই ইনপুট দেয়া হোক, কমপ্লেক্সিটি প্রায় একই রকম থাকবে। তাই বেশীরভাগ ক্ষেত্রে এ ধরণের কোডই সবচেয়ে বেশী কার্যকর হয়। তবে কিছু ক্ষেত্রে কমপ্লেক্সিটি O(1/g(n)) পর্যন্তও করা যায়। সেক্ষেত্রে অবশ্যই O(1/g(n)) এর থেকে O(1) বড়।
O(log(n)) এর কমপ্লেক্সিটি
এ ধরণের এলগোরিদমের কমপ্লেক্সিটি তুলনামূলকভাবে অনেক কম। যদিও এটি কন্সট্যান্ট কমপ্লেক্সিটির থেকে বেশী, কিন্তু অন্যান্য প্রায় যেকোন কমপ্লেক্সিটির থেকে এটি কম। যেহেতু এখানে n এর জন্য কমপ্লেক্সিটি কমে log(n) গুণ হয়ে যাচ্ছে, তাই এ ধরণের এলগোরিদম খুবই দ্রুত এবং কম মেমোরিতেই কাজ করতে পারে।
পলিনমিয়ালের কমপ্লেক্সিটি
এ ধরণের এলগোরিদমে কমপ্লেক্সিটি মূলত n এর কোন পলিনমিয়ালের প্রায় সমান হয়। যেমন : O(n2), O(n4) ইত্যাদি। এদের কমপ্লেক্সিটির তুলনা করা খুবই সহজ। যেমন O(n4) অবশ্যই O(n2) এর থেকে বড় হবে।
এক্সপোনেনশিয়ালের কমপ্লেক্সিটি
এ ধরণের এলগোরিদমের ক্ষেত্রে n সংখ্যক ইনপুটের জন্য Big O পাওয়া যায়, O(2n). যেহেতু n সবসময়ই পজিটিভ ভ্যালু, তাই পলিনমিয়ালের থেকে এক্সপোনেনশিয়ালের কমপ্লেক্সিটি বেশী। এক্সপোনেনশিয়ালের ক্ষেত্রে 2 কে বেস ধরা হয় কারণ কম্পিউটারকে সকল নির্দেশ বাইনারী সংখ্যারূপে দেয়া হয়। কিন্তু কোএফিসিয়েন্ট পরিবর্তনও করা যেতে পারে। তবে যদি কোএফিসিয়েন্ট জানা না থাকে, সেক্ষেত্রে এর মান সাধারণত 2 ধরা হয়।
ফ্যাক্টোরিয়ালের কমপ্লেক্সিটি
ফ্যাক্টোরিয়ালের কমপ্লেক্সিটি পলিনমিয়াল বা এক্সপোনেনশিয়াল সবকিছুর থেকেই বেশী। গামা ফাংশন নিয়ে একটু ধারণা থাকলে সহজেই বুঝা যায়। তবে গামা ফাংশন না বুঝলেও এইটুক আমরা সবাই বুঝি যে ফ্যাক্টোরিয়ালের ক্ষেত্রে গুণ হওয়া সংখ্যার পরিমাণ অধিক এবং এরা ক্রমবর্ধমান। n এর মান 5 হলে, n2 এর ক্ষেত্রে এর মান 25, 2n এর ক্ষেত্রে এর মান 32, এবং n! এর মান 120. তাই এটা খুব সহজেই বুঝা যায় যে কমপ্লেক্সিটি ফ্যাক্টোরিয়াল হারে বর্ধমান হলে এলগোরিদমেটি অনেক বেশী কম্পলেক্স হয়ে যায়।
আরও পড়ুনঃ What You Should Know About Blockchain
টাইম এবং স্পেস কমপ্লেক্সিটি
টাইম কমপ্লেক্সিটি নির্দেশ করে একটি এলগোরিদম কোন ইনপুটের সাপেক্ষে কত বেশী সময় নিবে। অন্যদিকে স্পেস কমপ্লেক্সিটি নির্দেশ করে কোন ইনপুটের সাপেক্ষে এলগোরিদমটি কতটুকু স্পেস নিবে। টাইম কমপ্লেক্সিটি এবং স্পেস কমপ্লেক্সিটি প্রায় একইরকম ভাবে কাজ করে। তবে তার মানে কখনোই এই নয় যে একই কোডের জন্য টাইম বা স্পেস কমপ্লেক্সিটি একই রকম হবে।
সর্টিং নিয়ে ধারণা থাকলে কুইক সর্ট এর কথা হয়তো শুনে থাকতে পারেন। এটি পার্টিশনের মাধ্যমে সর্টিং করে থাকে। তবে এর ক্ষেত্রে মেমোরির কমপ্লেক্সিটি O(nlog(n)) হলেও টাইম কমপ্লেক্সিটি O(n2)। কাজেই আমরা দেখতে পাচ্ছি যে এই এলগোরিদমটির জন্য মেমোরি কম লাগলেও সময় একটু বেশীই লাগে।
কোন এলগোরিদম যাচাই এর ক্ষেত্রে টাইম এবং স্পেস দুই ধরণের কমপ্লেক্সিটিকেই মাথায় রেখে আগাতে হয়। অন্যথায় কোড নির্দিষ্ট সিস্টেমের জন্য কাজ নাও করতে পারে।
Best, Average এবং Worst কমপ্লেক্সিটি
যেকোন এলগোরিদম সবসময় সব রকমের ইনপুটের ক্ষেত্রে একইভাবে কাজ করেনা। কিছু ক্ষেত্রে এটি খুব ভাল কাজ করে, কিছু ক্ষেত্রে খুব খারাপ, আবার কিছু ক্ষেত্রে মাঝারী। এবং এলগোরিদম তৈরীর সময় সব রকমের পরিস্থিতির কথা বিবেচনা করেই সেটি তৈরী করতে হয়। একটি উদাহরণ দিলে এটি আরো পরিষ্কার হয়ে যাবে।
সর্টিং এলগোরিদম এর মধ্যে কুইক সর্ট অনেক জনপ্রিয় একটি এলগোরিদম। যখন এর মধ্যে ইনপুটটি এমনভাবে দেয়া যে সব সংখ্যা আগে থেকেই সর্ট করা, তাহলে এটি খুব সহজেই সবচেয়ে ক্ষুদ্র সংখ্যা খুঁজে পেয়ে যাবে এবং এক্ষেত্রে কম্প্লেক্সিটি O(n log(n))। অর্থাৎ, অনেক কম কম্প্লেক্সিটি নিয়েই কোডটি সমস্যার সমাধান করে ফেলে।
কিন্তু যখন কেইসটি উল্টো তখন আসলে পরিস্থিতি কেমন হবে? যদি এটি নিম্নক্রমানুসারে সর্ট করা থাকে, সেক্ষেত্রে কিন্তু ক্ষুদ্রতম সংখ্যাটি Array তে সবার শেষে বসে আছে। এক্ষেত্রে Array এর প্রতিটা সংখ্যার জন্য বার বার অনেক বড় অপারেশন চালাতে হয়। তাই এক্ষেত্রে কম্প্লেক্সিটি O(n2) হয়ে যায়। এর মাঝামাঝি অবস্থার জন্য সবক্ষেত্রেই কম্প্লেক্সিটি O(n log(n)) .
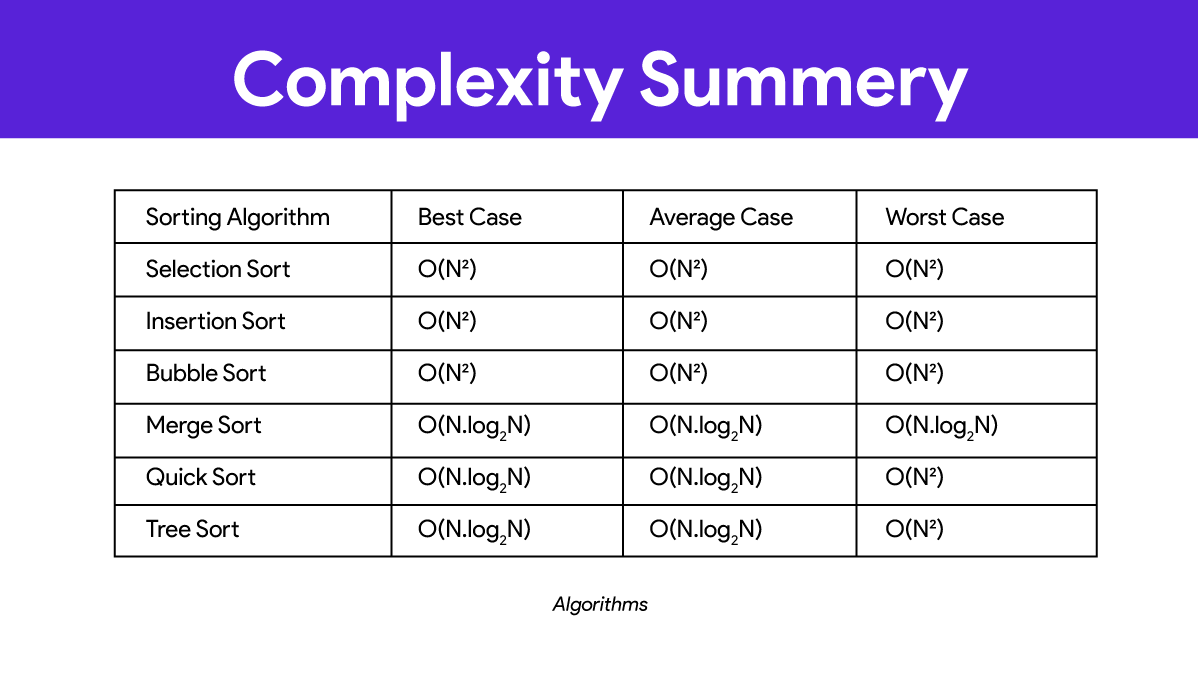
Best, Average এবং Worst Case এর জন্য বিভিন্ন এলগোরিদমের Big O Notation এর উদাহরণ :
প্রোগ্রামিংয়ের তুমুল প্রতিযোগিতার জগতে টেকার জন্য যেকোন এলগোরিদমের কমপ্লেক্সিটি সম্পর্কে ধারণা থাকা আবশ্যক। Big O notation যদিও কমপ্লেক্সিটির পূর্ণ এনালাইসিস নয়। কমপ্লেক্সিটির খুঁটিনাটি বুঝতে হলে Big O এর পাশাপাশি Omega, Theta এসব নিয়েও ধারণা থাকা জরুরী।
তবে যারা কোডিং এর জগতে একদমই নতুন, তাদের ক্ষেত্রে Big O দিয়েই কমপ্লেক্সিটি এনালাইসিস করা অনেক বেশী সহজ এবং সুবিধাজনক। আশা করি এ আর্টিকেলটি পড়ে শুধু প্রোগ্রামারই নয়, কোডিংয়ে আগ্রহী সকলেই উপকৃত হবেন। যাদের কমপ্লেক্সিটি নিয়ে কোন ধারণা নেই, তাদের Big O এর মাধ্যমে কমপ্লেক্সিটি এনালাইসিস সম্পর্কে ধারণা দেয়াই আর্টিকেলটির উদ্দেশ্যে।
বহুব্রীহির প্রোগ্রামিং কোর্সগুলো দেখতে এখানে ক্লিক করুন


